6.1 População e amostra. Unidade Estatística
Na maior parte dos estudos estatísticos é necessário tirar conclusões gerais acerca de um grande conjunto de individuos - população- baseando-nos num número restrito desses individuos -amostra.
População - Conjunto de unidades individuais, que podem ser pessoas, animais ou resultados experimentais, com uma ou mais caracteristicas em comum, que se pretendem analisar.
Amostra: Parte da população que é observada com o objectivo de obter informações para estudar para estudar a característica pretendida.
Cada elemento da população é uma unidade estatística.
Dimensão da amostra: É o número de elementos da amostra e, normalmente representa-se por "n."
A maior parte dos estudos estatísticos é baseada em amostras e isso deve-se fundamentalmente a pelo menos uma das seguintes razões:
População - Conjunto de unidades individuais, que podem ser pessoas, animais ou resultados experimentais, com uma ou mais caracteristicas em comum, que se pretendem analisar.
Amostra: Parte da população que é observada com o objectivo de obter informações para estudar para estudar a característica pretendida.
Cada elemento da população é uma unidade estatística.
Dimensão da amostra: É o número de elementos da amostra e, normalmente representa-se por "n."
A maior parte dos estudos estatísticos é baseada em amostras e isso deve-se fundamentalmente a pelo menos uma das seguintes razões:
- a população ser infinita;
- o estudo da população poder conduzir à sua destruição
- o estudo da população ter custos muito elevados
6.2 Censos e sondagens
Num censo ou recenseamento é feita a análise de todos os elementos da população em causa e tem-se por objetivo não só a enumeração dos seus elementos, como também o estudo de características importantes.
A alternativa à realização de um censo é uma sondagem.
Censo ou recenseamento – é um estudo estatístico de um universo de pessoas, instituição ou objetos físicos com o propósito de adquirir conhecimentos, observando todos os seus elementos e fazer juízos quantitativos acerca de características importantes desse universo.
Sondagem – é um estudo científico de uma parte da população com o objetivo de melhor conhecer atitudes, hábitos e preferências da população relativamente a acontecimentos, circunstâncias e assuntos de interesse comum.
A realização de sondagens é tão habitual nas sociedades atuais que podemos dizer que elas se relacionam, em maior ou menor grau, com a vida da generalidade das pessoas. Por exemplo, recorrendo a especializadas, os partidos políticos encomendam sondagens para estimar o número de votantes e/ou para avaliar o impacto público das suas posições, as empresas promovem sondagens para ver o número de compradores dos seus produtos e os investigadores efectuam sondagens para avaliar o impacto social das suas descobertas.
6.3 Considerações gerais sobre técnicas de amostragem
Existem vários tipos de amostragem dependendo dos parâmetros.
Eles são:Suponhamos que temos uma escola com 125 alunos e uma amostra de 30 alunos.
Amostragem aleatória simples
É toda a amostra em que a probabilidade de qualquer outro conjunto de n elementos da população ser selecionado é a mesma.
Exemplo:
Escrevem-se os 125 nomes dos respetivos alunos em 125 papéis; dobram-se os papéis; metem-se numa caixa e baralham-se; uma pessoa tira, aleatoriamente, um a um, 30 alunos.
Amostragem aleatória sistemática
Escolhe-se aleatoriamente um elemento x de entre os k primeiros, onde k é a parte inteira do quociente . A partir de x escolhem-se sucessivamente os elementos, x + k , x + 2k , …
Exemplo:
Ordenam-se todos os indivíduos da população; depois considera-se o quociente 125:30 = 4,1666… e escolhe-se um aluno ao acaso entre os 4 (parte inteira do quociente) primeiros da lista ordenada, por exemplo, o 3; continua-se a seleção, escolhendo todos os alunos da lista distanciados de 4 alunos até obtermos os 30 alunos da amostra.
Amostragem estratificada ou proporcional
Nesta amostragem a população é dividida em classes homogéneas, chamadas estratos.
Feitos os estratos, a amostra escolhe-se aleatoriamente em número proporcional ao número de elementos de cada estrato.
Exemplo:
125 – 30 125 – 30 125 - 30
80 – x 50 – x 70 – x
x = 19,2 x = 3,6 x = 7,2
Então, selecionar-se-iam 19 alunos da zona A, 4 da zona B e 7 da zona C.
Amostragem por grupos (clusters)
A população é dividida em clusters, onde cada cluster é representativo da população.
Seleciona-se aleatoriamente um conjunto de clusters e a amostra é constituída por todos os elementos dos clusters selecionados.
Exemplo:
Suponhamos que pretendíamos saber a satisfação das empresas de Lisboa.
Não dispondo de uma lista de todas as empresas, considera-se uma lista de todas as empresas (clusters) e a partir dela selecionam-se aleatoriamente alguns empresários, considerando-se a amostra constituída pelos empresários das empresas selecionadas.
Amostragem multietapas
A população é dividida em vários grupos e selecionam-se aleatoriamente alguns dos grupos. Por sua vez, estes grupos ainda estão divididos em grupos dos quais se selecionam alguns aleatoriamente.
O processo repete-se até ser possível continuar a constituir grupos.
Exemplo:
Para uma sondagem eleitoral considera-se Portugal dividido em regiões, dentro de cada região estimam-se os grupos de centros populacionais com dimensão semelhante, selecionam-se aleatoriamente algumas destas cidades, as cidades são divididas em freguesias e algumas das freguesias são selecionadas aleatoriamente. No fim, em cada freguesia são escolhidos alguns elementos da população para inquirir.
Eles são:Suponhamos que temos uma escola com 125 alunos e uma amostra de 30 alunos.
Amostragem aleatória simples
É toda a amostra em que a probabilidade de qualquer outro conjunto de n elementos da população ser selecionado é a mesma.
Exemplo:
Escrevem-se os 125 nomes dos respetivos alunos em 125 papéis; dobram-se os papéis; metem-se numa caixa e baralham-se; uma pessoa tira, aleatoriamente, um a um, 30 alunos.
Amostragem aleatória sistemática
Escolhe-se aleatoriamente um elemento x de entre os k primeiros, onde k é a parte inteira do quociente . A partir de x escolhem-se sucessivamente os elementos, x + k , x + 2k , …
Exemplo:
Ordenam-se todos os indivíduos da população; depois considera-se o quociente 125:30 = 4,1666… e escolhe-se um aluno ao acaso entre os 4 (parte inteira do quociente) primeiros da lista ordenada, por exemplo, o 3; continua-se a seleção, escolhendo todos os alunos da lista distanciados de 4 alunos até obtermos os 30 alunos da amostra.
Amostragem estratificada ou proporcional
Nesta amostragem a população é dividida em classes homogéneas, chamadas estratos.
Feitos os estratos, a amostra escolhe-se aleatoriamente em número proporcional ao número de elementos de cada estrato.
Exemplo:
125 – 30 125 – 30 125 - 30
80 – x 50 – x 70 – x
x = 19,2 x = 3,6 x = 7,2
Então, selecionar-se-iam 19 alunos da zona A, 4 da zona B e 7 da zona C.
Amostragem por grupos (clusters)
A população é dividida em clusters, onde cada cluster é representativo da população.
Seleciona-se aleatoriamente um conjunto de clusters e a amostra é constituída por todos os elementos dos clusters selecionados.
Exemplo:
Suponhamos que pretendíamos saber a satisfação das empresas de Lisboa.
Não dispondo de uma lista de todas as empresas, considera-se uma lista de todas as empresas (clusters) e a partir dela selecionam-se aleatoriamente alguns empresários, considerando-se a amostra constituída pelos empresários das empresas selecionadas.
Amostragem multietapas
A população é dividida em vários grupos e selecionam-se aleatoriamente alguns dos grupos. Por sua vez, estes grupos ainda estão divididos em grupos dos quais se selecionam alguns aleatoriamente.
O processo repete-se até ser possível continuar a constituir grupos.
Exemplo:
Para uma sondagem eleitoral considera-se Portugal dividido em regiões, dentro de cada região estimam-se os grupos de centros populacionais com dimensão semelhante, selecionam-se aleatoriamente algumas destas cidades, as cidades são divididas em freguesias e algumas das freguesias são selecionadas aleatoriamente. No fim, em cada freguesia são escolhidos alguns elementos da população para inquirir.
7 - Análise, representação e redução de dados
7.1 Variáveis estatísticas. Variáveis qualitativas e quantitativas
Cada elemento de uma unidade estatística tem muitos caracteres, características ou atributos a que chamamos variáveis.
Variável estatística qualitativa – É uma variável que assume diversas modalidades, categorias ou outras características, não suscetíveis de medição, mas sim de classificação.
Exemplo:
Variável estatística quantitativa – Uma variável diz-se quantitativa (ou numérica) se se referir a uma característica que se possa contar ou medir.
Exemplo:
Variável estatística qualitativa – É uma variável que assume diversas modalidades, categorias ou outras características, não suscetíveis de medição, mas sim de classificação.
Exemplo:
Variável estatística quantitativa – Uma variável diz-se quantitativa (ou numérica) se se referir a uma característica que se possa contar ou medir.
Exemplo:
7.2 Variáveis quantitativas discretas e contínuas
Quando as variáveis estatísticas são quantitativas, pode-se ainda dividi-las em dois grupos:discretas ou contínuas.
Variável quantitativa discreta – São as variáveis quantitativas de contagem, isto é, as que se referem a características que só se podem contar e não se podem medir.
Exemplo:
A variável “número de irmãos” caracteriza-se “discreta” porque mesmo antes de se fazer uma observação, sabe-se que se vão encontrar dados estatísticos que, em termos geométricos, seriam representados na reta real por pontos isolados em número finito ou infinito.
Variável quantitativa contínua – São as variáveis quantitativas de medição, isto é, as que se podem medir.
Exemplo:
A variável “altura dos alunos” caracteriza-se “contínua” porque mesmo antes de se fazer uma observação, sabe-se que se podem encontrar dados estatísticos que, em termos geométricos, seriam representados na reta real por qualquer ponto de um intervalo.
Variável quantitativa discreta – São as variáveis quantitativas de contagem, isto é, as que se referem a características que só se podem contar e não se podem medir.
Exemplo:
A variável “número de irmãos” caracteriza-se “discreta” porque mesmo antes de se fazer uma observação, sabe-se que se vão encontrar dados estatísticos que, em termos geométricos, seriam representados na reta real por pontos isolados em número finito ou infinito.
Variável quantitativa contínua – São as variáveis quantitativas de medição, isto é, as que se podem medir.
Exemplo:
A variável “altura dos alunos” caracteriza-se “contínua” porque mesmo antes de se fazer uma observação, sabe-se que se podem encontrar dados estatísticos que, em termos geométricos, seriam representados na reta real por qualquer ponto de um intervalo.
7.3 Tabelas de frequência para dados qualitativos ou quantitativos discretos
Para construirmos uma tabela de frequências precisamos de realizar dois cálculos importantes, a saber:
Frequência absoluta – A frequência absoluta de uma categoria, classe ou valor é o número de elementos da amostra iguais a cada uma das categorias. Representa-se por ni.
Frequência relativa – A frequência relativa é igual ao quociente entre a frequência absoluta e o número total de dados na amostra em estudo. Representa-se fi.
A frequência absoluta acumulada (Ni) e a frequência relativa acumulada (Fi) obtêm-se adicionando as frequências absolutas e relativas, respetivamente, até ao valor considerado da variável estatística.
Exemplo:
Frequência absoluta – A frequência absoluta de uma categoria, classe ou valor é o número de elementos da amostra iguais a cada uma das categorias. Representa-se por ni.
Frequência relativa – A frequência relativa é igual ao quociente entre a frequência absoluta e o número total de dados na amostra em estudo. Representa-se fi.
A frequência absoluta acumulada (Ni) e a frequência relativa acumulada (Fi) obtêm-se adicionando as frequências absolutas e relativas, respetivamente, até ao valor considerado da variável estatística.
Exemplo:
7.4 Tabela de frequências para dados contínuos
No caso de os dados serem de natureza contínua a construção da tabela de frequências não é tão simples como no caso dos dados discretos, pois é necessário definir previamente o número de classes.
[1,80 ; 1,85[ - representa uma classe em que 1,80 é o limite inferior da classe; 1,85 é o limite superior da classe, 1,85-1,80 = 0,05 é a amplitude da classe e 1,80 + 1,85/2 = 1,83 é a marca da classe.
Normalmente, para determinar o número de classes de um conjunto de dados usa-se a regra de Sturges
Regra de Sturges – Para organizar uma amostra, de dados contínuos, de dimensão n pode considerar-se para números de classes o valor k onde k é o menor número inteiro tal que 2k > n .
Temos como exemplo:
A massa, em gramas, de 50 pães produzidos numa padária foi registada na seguinte tabela:
Primeiramente, temos de determinar o número de classes que se irá usar na tabela:
n = 50 ; < 50 e > 50 – 6 classes
Depois, temos de determinar a amplitude de cada classe (diferença entre o valor máximo e mínimo):
29 (nº maior) – 18 (nº menor) = 11 e 11:6 (nº de classes) = 1,8 consideremos 2 para amplitude de classe.
[1,80 ; 1,85[ - representa uma classe em que 1,80 é o limite inferior da classe; 1,85 é o limite superior da classe, 1,85-1,80 = 0,05 é a amplitude da classe e 1,80 + 1,85/2 = 1,83 é a marca da classe.
Normalmente, para determinar o número de classes de um conjunto de dados usa-se a regra de Sturges
Regra de Sturges – Para organizar uma amostra, de dados contínuos, de dimensão n pode considerar-se para números de classes o valor k onde k é o menor número inteiro tal que 2k > n .
Temos como exemplo:
A massa, em gramas, de 50 pães produzidos numa padária foi registada na seguinte tabela:
Primeiramente, temos de determinar o número de classes que se irá usar na tabela:
n = 50 ; < 50 e > 50 – 6 classes
Depois, temos de determinar a amplitude de cada classe (diferença entre o valor máximo e mínimo):
29 (nº maior) – 18 (nº menor) = 11 e 11:6 (nº de classes) = 1,8 consideremos 2 para amplitude de classe.
7.5 Representação gráfica. Gráficos de barras
A representação gráfica é um tema complexo onde se intersectam áreas diversas como a estatística, a psicologia e o desenho.
Um gráfico pode estar correto do ponto de vista estatístico, mas não ser atrativo nem de leitura fácil.
Exemplo:
Gráfico de barras verticais
Gráfico de barras simples horizontais:
Vantagens:
Gráfico de barras agrupadas:
Vantagens:
Sobreposição em gráfico de barras:
Vantagens:
Vantagens:
Desvantagens:
Um gráfico pode estar correto do ponto de vista estatístico, mas não ser atrativo nem de leitura fácil.
Exemplo:
Gráfico de barras verticais
Gráfico de barras simples horizontais:
Vantagens:
- Permite estabelecer comparações facilmente.
- Tem forte impacto visual.
- Só pode ser usado para transmitir informações simples.
Gráfico de barras agrupadas:
- Permite comparar diferentes grupos de dados para os mesmos valores da variável.
- Não pode ser utilizado para variáveis que apresentam muitas modalidades.
Sobreposição em gráfico de barras:
Vantagens:
- Em grupos diferentes de dados permite comparar valores da mesma modalidade e comparar totais relativos a cada modalidade.
- Poucos grupos de dados podem ser utilizados.
7.6 Gráficos circulares
Os gráficos circulares são uma boa forma de mostrar como um todo está repartido.
- A amplitude de cada setor é proporcional à frequência que representa;
- A legenda pode ser dispensada, inscrevendo-se os valores da variável e as suas frequências juntos dos respetivos setores circulares a que se referem;
- Podem-se usar cores diferentes para os diferentes setores; o gráfico deve ter um título adequado.
Temos como exemplo:
Vantagens:
- É útil quando a análise das proporções é mais importante do que o valor real. Tem um forte impacto visual.
Desvantagens:
- Só pode ser usado quando a variável toma poucos valores. Um só um gráfico não permite comparar dois grupos de dados.
7.7 Pictogramas
Os pictogramas são gráficos muito semelhantes aos gráficos de barras. A única diferença reside no facto de se utilizarem símbolos mais atraentes alusivos à situação concreta em estudo.
- Indicar no gráfico o significado de cada símbolo;
- Utilizar símbolos sugestivos em relação à variável estatística em estudo;
- Utilizar sempre o mesmo símbolo;
- Desenhar os símbolos em linhas ou colunas;
- Espaçar igualmente os símbolos;
- Expressar as diferentes frequências através de um maior ou menor número de símbolos, não aumentando ou diminuindo o tamanho do símbolo;
- O gráfico deve ter um título adequado.
Temos como exemplos:
Vantagens:
- Muito atrativo.
- Grande impacto visual.
Desvantagens:
- Dá pouca informação.
- Pouca precisão.
7.8 Função cumulativa para dados discretos
As frequências acumuladas são representadas graficamente pela função cumulativa.
A função cumulativa indica, para cada valor real x, a frequência absoluta (ou relativa) de observações menores ou iguais a x.
Exemplo:
A 20 trabalhadores de uma empresa perguntou-se qual era a despesa que tinha, em euros, por semana, em transportes públicos.
Os dados obtidos foram
A função cumulativa indica, para cada valor real x, a frequência absoluta (ou relativa) de observações menores ou iguais a x.
Exemplo:
A 20 trabalhadores de uma empresa perguntou-se qual era a despesa que tinha, em euros, por semana, em transportes públicos.
Os dados obtidos foram
:
N (x) = 0 se x <14
4 se 14 < x < 15
11 se 15 < x < 16
16 se 16 < x < 17
18 se 17 < x < 18
19 se 18 < x < 19
20 se x > 19
E obtemos uma representação gráfica deste tipo:
N (x) = 0 se x <14
4 se 14 < x < 15
11 se 15 < x < 16
16 se 16 < x < 17
18 se 17 < x < 18
19 se 18 < x < 19
20 se x > 19
E obtemos uma representação gráfica deste tipo:
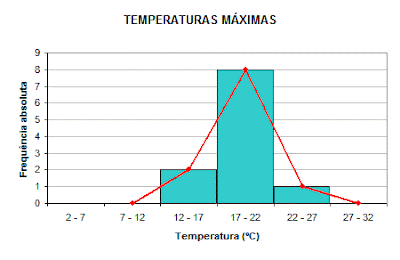
7.9 Histograma
No caso de uma variável contínua é muito frequente representar graficamente os dados através de um histograma.
- O gráfico deve ter um título adequado;
- Os dados estão agrupados em classes (sejam contínuos ou discretos);
- A área da barra retangular é proporcional à frequência;
- Os diferentes valores da variável estão representados no eixo horizontal que está dividido numa escala contínua como um eixo cartesiano;
- No eixo vertical estão representadas as frequências das classes;
- As barras são desenhadas verticalmente e correspondem a cada uma das classes em que os valores foram agrupados;
- Não há espaço entre as barras.
Temos como exemplos:
Vantagens:
- Para determinadas situações é a única forma correta de apresentar os dados.
- O histograma dá a ideia da forma como se distribuem os dados.
Desvantagens:
- Difícil construção quando a amplitude dos intervalos é diferente. Com as calculadoras gráficas ou computadores este problema é ultrapassado.
7.10 Polígonos de frequências para dados agrupados em classes
O polígono de frequências para dados agrupados em classes resulta da união sucessiva, através de segmentos de recta, dos pontos médios dos lados superiores dos diferentes retângulos de um histograma.
Para a sua construção, localiza-se o ponto cuja abcissa é igual ao ponto médio da classe e a ordenada é a correspondente à frequência da classe. Unem os sucessivos pontos formando um polígono. De modo a obter uma figura fechada, juntam-se classes extra, uma de cada lado, de frequência zero.
Temos como exemplos: Vantagens:
Para a sua construção, localiza-se o ponto cuja abcissa é igual ao ponto médio da classe e a ordenada é a correspondente à frequência da classe. Unem os sucessivos pontos formando um polígono. De modo a obter uma figura fechada, juntam-se classes extra, uma de cada lado, de frequência zero.
Temos como exemplos: Vantagens:
- Permite comparar histogramas utilizando apenas os respetivos polígonos de frequência no mesmo quadro.
- Difícil construção manual. Usando tecnologia este problema fica ultrapassado.
7.11 Função cumulativa para dados agrupados em classes
Exemplo:
Tabela relativa a uma amostra da massa, em quilogramas, de 50 abóboras.
O limite inferior da segunda classe é o 6 e a frequência acumulada é a frequência da classe anterior, ou seja, 0,1.
Admitindo que a frequência se distribui uniformemente sobre a classe, une-se o ponto de coordenadas (3 , 0) com o ponto de coordenadas (6 ; 0,1).
Procede-se de modo idêntico até se chegar à última classe.
O gráfico continua com o segmento ao eixo Ox pois sabemos que a frequência relativa acumulada correspondente ao seu limite superior é igual a 1.
Tabela relativa a uma amostra da massa, em quilogramas, de 50 abóboras.
O limite inferior da segunda classe é o 6 e a frequência acumulada é a frequência da classe anterior, ou seja, 0,1.
Admitindo que a frequência se distribui uniformemente sobre a classe, une-se o ponto de coordenadas (3 , 0) com o ponto de coordenadas (6 ; 0,1).
Procede-se de modo idêntico até se chegar à última classe.
O gráfico continua com o segmento ao eixo Ox pois sabemos que a frequência relativa acumulada correspondente ao seu limite superior é igual a 1.
7.12 Diagrama de caule-e-folhas
Esta forma de organização de dados tem a particularidade de permitir ao observador uma perceção do aspeto global da forma como os dados se distribuem sem que, ao mesmo tempo, se perca a informação.
Separa-se o dígito das dezenas, a que chamamos caule, do dígito das unidades, a que chamamos folha.
Exemplo:
Vantagens:
Desvantagens:
Separa-se o dígito das dezenas, a que chamamos caule, do dígito das unidades, a que chamamos folha.
Exemplo:
Vantagens:
- Todos os dados da amostra aparecem no gráfico.
- Dá uma interpretação visual sobre a forma como os dados se distribuem.
- Permite ordenar rapidamente a amostra.
- Facilita a leitura ou a determinação de medidas estatísticas.
- É muito sugestivo para comparar duas amostras.
- Não é necessário construir previamente uma tabela de frequências.
Desvantagens:
- Difícil construção quando a amplitude dos intervalos é diferente. Com as calculadoras ou computadores este problema é ultrapassado.
7.13 Considerações gerais sobre representações gráficas
No dia-a-dia encontramos muitos outros tipos de gráficos dos que os que foram apresentados neste capítulo.
Exemplos:
Exemplos:
Gráficos de linhas ou cronogramas
Pirâmides etárias
8 - Medidas de Localização
8.1 Média para dados simples e dados agrupados
Média – A média de um conjunto de dados numéricos é o quociente entre a soma de todos os elementos da amostra e o número de elementos da amostra.
Exemplo:
A Ana registou o número de vezes que ligava para o namorado por dia durante o mês de Maio.
1 x 1 + 6 x 2 + 5 x 3 + 4 x 4 + 4 x 5 + 5 x 6 + 3 x 7 + 2 x 8 / 30 = 131/30 = 4,4
Em média, a Rita ligou para o namorado 4,4 vezes por dia.
Exemplo:
A Ana registou o número de vezes que ligava para o namorado por dia durante o mês de Maio.
1 x 1 + 6 x 2 + 5 x 3 + 4 x 4 + 4 x 5 + 5 x 6 + 3 x 7 + 2 x 8 / 30 = 131/30 = 4,4
Em média, a Rita ligou para o namorado 4,4 vezes por dia.
8.2 Média aproximada para dados agrupados em intervalos
Ao calcular a média a partir de dados agrupados, em que as classes são intervalos, não se obtém o valor exato da média, mas sim um valor aproximado. Assim, se os dados estão agrupados em classes, o valor aproximado da média calcula-se usando as fórmulas anteriores, mas considerando xi o ponto médio da classe i.
Exemplo:O pai da Adriana disse-lhe que ela está sempre a fazer zapping enquanto ela tenta ver a novela.
Para mostrar ao pai que está errado, a Adriana registou o número de vezes que fez zapping durante os 31 dias do mês passado e calculou a média:
x = 342/31 = 11,05
A Adriana fez zapping aproximadamente 11 vezes por dia, durante um mês.
Exemplo:O pai da Adriana disse-lhe que ela está sempre a fazer zapping enquanto ela tenta ver a novela.
Para mostrar ao pai que está errado, a Adriana registou o número de vezes que fez zapping durante os 31 dias do mês passado e calculou a média:
x = 342/31 = 11,05
A Adriana fez zapping aproximadamente 11 vezes por dia, durante um mês.
8.3 Utilização da calculadora gráfica para obter a média
Podemos usar a calculadora gráfica para calcular a média para os dados simples ou dados agrupados em classes.
Exemplo:
Em L1 colocamos o número de primos e em L2 as frequências absolutas
Seguidamente fazemos “stat” e selecionamos a opção “calc” em que escolhemos a primeira opção “1 – Var Stats”
Finalmente, indicamos as listas que queremos ver a variável estatística e carregamos “enter” e irá aparecer-nos, logo em primeiro, a média entre outros..:
Neste caso a média é 1,48
Exemplo:
Em L1 colocamos o número de primos e em L2 as frequências absolutas
8.4 Propriedades da média
Propriedade 1:
Adicionando um valor constante a cada um dos elementos de um conjunto de números, a média vem adicionada a essa constante.
Exemplo:
O Rodrigo decidiu aumentar três valores a cada uma das classificações dos seus alunos. A média dos resultados finais, depois deste aumento, vem acrescida de três valores
Propriedade 2:
Multiplicando cada elemento de um conjunto de números por uma constante, a média vem multiplicada por essa constante.
Propriedade 3:
Dados dois conjuntos de números, com o mesmo número n de elementos, de médias x e x1 respetivamente, o conjunto obtido pela soma dos elementos dos conjuntos dados, um a um, é um conjunto de n números de média x + x1 .
A Anabela no teste a seguir decidiu aumentar 20% a cada uma das notas dos seus alunos. A média dos resultados finais, depois deste aumento, bem multiplicada por 1,2 (x + 0,2x =1,2x)
Adicionando um valor constante a cada um dos elementos de um conjunto de números, a média vem adicionada a essa constante.
Exemplo:
O Rodrigo decidiu aumentar três valores a cada uma das classificações dos seus alunos. A média dos resultados finais, depois deste aumento, vem acrescida de três valores
Propriedade 2:
Multiplicando cada elemento de um conjunto de números por uma constante, a média vem multiplicada por essa constante.
Propriedade 3:
Dados dois conjuntos de números, com o mesmo número n de elementos, de médias x e x1 respetivamente, o conjunto obtido pela soma dos elementos dos conjuntos dados, um a um, é um conjunto de n números de média x + x1 .
A Anabela no teste a seguir decidiu aumentar 20% a cada uma das notas dos seus alunos. A média dos resultados finais, depois deste aumento, bem multiplicada por 1,2 (x + 0,2x =1,2x)
8.5 Mediana para dados simples ou agrupados
Se x1 , x2 , … , xn representam n valores ordenados de uma variável quantitativa, chama-semediana e pode representar-se por Md .
- Se o valor da variável que ocupa a posição central é impar:
- Se o valor da variável que ocupa a posição central é par:
8.6 Classe mediana. Mediana aproximada para dados agrupados em intervalos
Para o cálculo de um valor aproximado da mediana admite-se que os valores se distribuem uniformemente em cada classe. Assim, aplica-se uma regra de três simples para o cálculo do valor aproximado da mediana.
Exemplo:
O Rodrigo, mediu os seus colegas da turma para determinar a mediana.
A classe mediana é [1,60 ; 1,65[
0,78 – 0,48 = 0,3 0,50 – 0,48 = 0,02
0,3 ----- 0,05 x = 0,0033
0,02 ----- x x = 1,60 + 0,033 = 1,6033
A mediana é, aproximadamente, 1,6033.
Exemplo:
O Rodrigo, mediu os seus colegas da turma para determinar a mediana.
A classe mediana é [1,60 ; 1,65[
0,78 – 0,48 = 0,3 0,50 – 0,48 = 0,02
0,3 ----- 0,05 x = 0,0033
0,02 ----- x x = 1,60 + 0,033 = 1,6033
A mediana é, aproximadamente, 1,6033.
8.7































Sem comentários:
Enviar um comentário